 |
|
Английский физик Питер В. Хиггс в начале |
 |
|
Вид детектора CMS перед закрытием 17 августа 2008 года. |
|
Содержание сайта =>> Популярно о науке =>> Физика |
«Успехи физических наук», 2012, т. 182, № 10, http://ufn.ru/ru/articles/2012/10/a/
«В защиту науки», 2012, № 11, http://www.ras.ru/digest/fdigestlist/bulletin.aspx
«Наука и жизнь», 2012, № 10, http://www.nkj.ru/archive/articles/21175/
В. А. Рубаков
Институт ядерных исследований РАН,
Московский государственный университет
Четвёртого июля 2012 года произошло событие, имеющее выдающееся значение для физики: на семинаре в ЦЕРНе (Европейском центре ядерных исследований) было объявлено об открытии новой частицы, которая, как осторожно заявляют авторы открытия, по своим свойствам соответствует теоретически предсказанному элементарному бозону Стандартной модели физики элементарных частиц. Его обычно называют бозоном Хиггса, хотя это название не вполне адекватно. Как бы то ни было, речь идёт об открытии одного из главных объектов фундаментальной физики, не имеющего аналогов среди известных элементарных частиц и занимающего уникальное место в физической картине мира 1.
|
|
1. Что было на семинаре и до него
Объявление о семинаре было сделано в конце июня, и сразу стало ясно, что будет он неординарным. Дело в том, что первые указания на существование нового бозона получили ещё в декабре 2011 года в экспериментах ATLAS и CMS, проводимых на Большом адронном коллайдере (LHC – Large Hadron Collider) в ЦЕРНе. Кроме того, незадолго до семинара появилось сообщение, что данные экспериментов на протон-антипротонном коллайдере Tevatron (Fermilab, США) также указывают на существование нового бозона. Всего этого было ещё недостаточно, чтобы говорить об открытии. Но с декабря количество данных, набранных на LHC, удвоилось и методы их обработки стали совершеннее. Результат оказался впечатляющим: в каждом из экспериментов ATLAS и CMS по отдельности статистическая достоверность сигнала достигла величины, которая в физике элементарных частиц считается уровнем открытия (пять стандартных отклонений).
Семинар прошёл в праздничной атмосфере. Помимо исследователей, работающих в ЦЕРНе, и студентов, занимающихся там по летним программам, его «посетили» с помощью интернета участники крупнейшей конференции по физике высоких энергий, которая как раз в этот же день открылась в Мельбурне. Семинар транслировали по интернету в научные центры и университеты всего мира, включая, конечно, Россию. После впечатляющих выступлений руководителей коллабораций CMS – Джо Инкандела и ATLAS – Фабиолы Джанотти генеральный директор ЦЕРНа Рольф Хойер заключил: «I think we have it!» («Думаю, он у нас в руках!»).
Так что же такое «у нас в руках» и зачем его придумали теоретики?
2. Что представляет собой новая частица
Минимальная версия теории микромира носит неуклюжее название Стандартной модели. Она включает все известные элементарные частицы (мы их перечислим ниже) и все известные взаимодействия между ними. Гравитационное взаимодействие стоит особняком: оно не зависит от типов элементарных частиц, а описывается общей теорией относительности Эйнштейна. Бозон Хиггса оставался единственным не открытым до последнего времени элементом Стандартной модели.
Мы назвали Стандартную модель минимальной именно потому, что других элементарных частиц в ней нет. В частности, в ней имеется один, и только один, бозон Хиггса, и он – частица элементарная, а не составная (о других возможностях речь пойдёт ниже). Большинство аспектов Стандартной модели – за исключением нового сектора, к которому принадлежит бозон Хиггса, – проверены в многочисленных экспериментах, и главная задача в программе работ LHC – выяснить, действительно ли в природе реализуется минимальный вариант теории и насколько полно она описывает микромир 2.
В ходе выполнения этой программы и была открыта новая частица, довольно тяжёлая по меркам физики микромира. В этой области науки массу измеряют в единицах энергии, имея в виду связь
Она не имеет электрического заряда, нестабильна и может распадаться
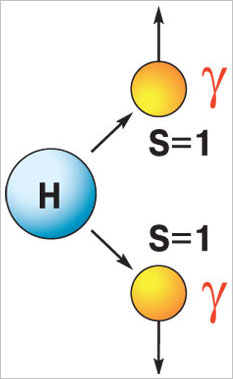 |
|
|
Рис. 1. Бозон Хиггса Н (спин 0) распадается на два фотона (спин 1), спины которых антипараллельны и в сумме дают 0 |
Вообще всё, что сейчас известно о новой частице, согласуется с её интерпретацией как бозона Хиггса, предсказанного простейшей версией теории элементарных частиц – Стандартной моделью. В рамках Стандартной модели можно вычислить как вероятность рождения бозона Хиггса в протон-протонных столкновениях на Большом адронном коллайдере, так и вероятности его распадов Н → γγ и Н → 4l, и тем самым предсказать число ожидаемых событий. Предсказания хорошо подтверждаются экспериментами, но, конечно, в пределах погрешностей. Экспериментальные погрешности ещё велики, да и измеренных величин пока совсем немного. Тем не менее трудно сомневаться, что открыт именно бозон Хиггса или
Более чем в половине случаев бозон Хиггса должен распадаться на пару
Все элементарные частицы обладают спином – внутренним угловым моментом. Спин частицы может быть целым (включая нуль) или полуцелым в единицах постоянной Планка ћ. Частицы с целым спином называются бозонами, с полуцелым – фермионами. Спин электрона равен 1/2, спин
Кроме того, он не равен единице: частица спина 1 не может распадаться на два фотона со спином 1. Остаётся спин 0; 2 или больше. Хотя спин новой частицы ещё не измерен, крайне маловероятно, что мы имеем дело с частицей спина 2 или больше. Почти наверняка спин H равен нулю, и, как мы увидим, именно таким должен быть бозон Хиггса.
Заканчивая описание известных свойств новой частицы, скажем, что живёт она по меркам физики микромира довольно долго. На основе экспериментальных данных оценка снизу её времени жизни даёт
3. Зачем нужен новый бозон?
В квантовой физике каждая элементарная частица является квантом некоторого поля, и наоборот, каждому полю соответствует своя частица-квант; наиболее известный пример – электромагнитное поле и его квант, фотон. Поэтому вопрос, поставленный в заглавии этого раздела, можно переформулировать так:
Зачем нужно новое поле и каковы его ожидаемые свойства?
Краткий ответ состоит в том, что симметрии теории микромира – будь то Стандартная модель или
Расшифровка этого короткого абзаца требует, конечно, рассмотрения, хотя бы в общих чертах, роли симметрий в физике микромира.
3.1. Симметрии, законы сохранения и запреты
Общим свойством физических теорий, будь то ньютонова механика, механика специальной теории относительности, квантовая механика или теория микромира, является то, что каждой симметрии соответствует свой закон сохранения. Например, симметрии относительно сдвигов во времени (законы физики одинаковы в каждый момент времени) соответствует закон сохранения энергии, симметрии относительно сдвигов в пространстве (все точки пространства равноправны) – закон сохранения импульса, а симметрии относительно поворотов в пространстве (все направления в пространстве равноправны) – закон сохранения углового момента. Законы сохранения можно интерпретировать и как запреты: перечисленные симметрии запрещают изменение энергии, импульса и углового момента замкнутой системы при её эволюции.
 |
|
|
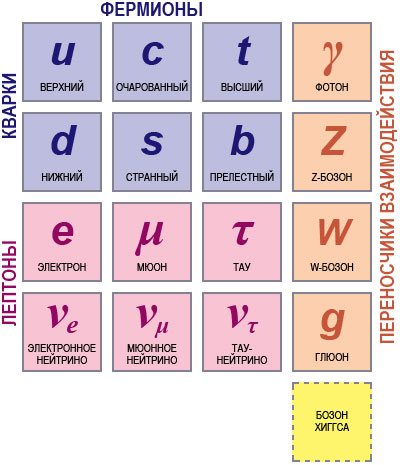
Рис. 2. Частицы Стандартной модели. |
Наоборот, каждому закону сохранения соответствует своя симметрия; это утверждение является точным в квантовой теории. Спрашивается: какая же симметрия соответствует закону сохранения электрического заряда? Ясно, что симметрии пространства и времени, о которых мы только что упомянули, здесь ни при чём. Тем не менее, такая симметрия имеется. Дело в том, что помимо очевидных, пространственно-временных симметрий существуют неочевидные, «внутренние» симметрии. Одна из них и приводит к сохранению электрического заряда. Для нас важно, что эта же внутренняя симметрия (только понимаемая в расширенном смысле – физики употребляют термин «калибровочная инвариантность») объясняет, почему у фотона нет массы. Отсутствие массы у фотона, в свою очередь, тесно связано с тем, что у света есть поляризация только двух типов – левая и правая.
Чтобы показать, насколько нетривиален факт наличия только двух типов поляризации света, отвлечёмся на время от разговора о симметриях и снова напомним, что элементарные частицы характеризуются спином, который может быть полуцелым или целым в единицах постоянной Планка ћ. Элементарные фермионы (частицы полуцелого спина) имеют спин 1/2. Это электрон e, электронное нейтрино νe , тяжёлые аналоги электрона – мюон μ и тау-лептон τ, их нейтрино νμ и ντ , кварки шести типов u, d, c, s, t, b и соответствующие всем им античастицы (позитрон e+, антинейтрино ν̃e , антикварк ũ и т. д.). Кварки u и d – лёгкие, и из них состоят протон (кварковый состав uud ) и нейтрон (udd ). Остальные кварки (c, s, t, b) – более тяжёлые; они входят в состав короткоживущих частиц, например,
К бозонам, частицам целого спина, относятся не только фотон, но и его отдалённые аналоги – глюоны (спин 1). Глюоны отвечают за взаимодействия между кварками и связывают их в протон, нейтрон и другие составные частицы. Кроме того, есть ещё три частицы спина 1 – электрически заряженные W +-,
Массивная частица спина s (в единицах ћ) имеет
3.2. Что-то не так!
 |
|
|
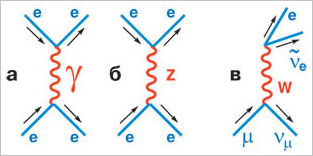
Рис. 3. Взаимодействия в микромире. |
Ключевыми для нас являются, однако, не фотоны, а W ±- и
Как мы уже говорили, каждый из W ±- и
Аналогия с электродинамикой простирается ещё дальше. Как и теория фотона, теория W ±- и
Дальше – больше. Слабые взаимодействия – взаимодействия электронов, нейтрино, кварков и других частиц с W ±- и
Чтобы пояснить суть проблемы, выключим сначала массу электрона (в теории такое позволено) и рассмотрим воображаемый мир, в котором масса электрона равна нулю. В таком мире электрон летал бы со скоростью света и мог иметь спин, направленный вдоль направления движения или против него. Так же как и для фотона, в первом случае мы говорили бы об электроне с правой поляризацией или, короче, о правом электроне, во втором – о левом электроне.
 |
|
|
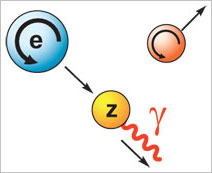
Рис. 4. При излучении фотона или испускании |
Поскольку мы хорошо знаем, как устроены электромагнитные и слабые взаимодействия (а только в них электрон и участвует), мы вполне способны описать свойства электрона в нашем воображаемом мире. А они таковы.
Подчеркнём, что в воображаемом мире с безмассовыми фермионами нет никаких проблем с тем, что левые и правые электроны взаимодействуют с W- и
Попробуем теперь включить массу электрона – и немедленно придём к противоречию. Быстро движущийся электрон, скорость которого близка к скорости света, а спин направлен против направления движения, выглядит почти так же, как левый электрон из нашего воображаемого мира. И взаимодействовать он должен почти так же 4. Если это взаимодействие связано с
Соответственно, и его
Это противоречие показывает, что симметрии Стандартной модели (для определённости будем говорить о ней, хотя всё сказанное относится к любому другому варианту теории) должны были бы запрещать существование масс не только у W ±- и
Таким образом, в мире, где все симметрии Стандартной модели реализовывались бы так же, как в электродинамике, все элементарные частицы должны были бы иметь нулевые массы. Но в реальном мире эти массы есть, значит, с симметриями Стандартной модели
3.3. Нарушение симметрии
 |
|
|
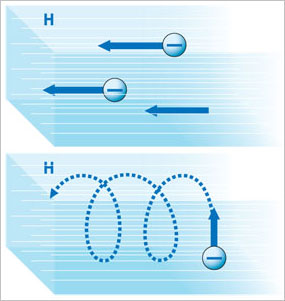
Рис. 5. В однородном магнитном поле электрон движется по прямой вдоль поля и по спирали в любом другом направлении. |
Говоря о связи симметрий с законами сохранения и запретами, мы упустили из виду одно обстоятельство. Оно заключается в том, что законы сохранения и симметрийные запреты выполняются только тогда, когда симметрия присутствует явно. Однако симметрии могут быть и нарушенными. Например, в однородном образце железа при комнатной температуре всегда имеется магнитное поле, направленное в
Здесь мы имеем дело со спонтанным нарушением симметрии. В отсутствие внешних воздействий (например, магнитного поля Земли) в разных образцах железа магнитное поле может быть направлено в разные стороны, и ни одно из этих направлений не будет предпочтительнее другого. Исходная симметрия относительно вращений
Итак, спонтанное нарушение некоторой симметрии имеет место тогда, когда уравнения теории симметричны, а основное состояние – нет. Слово «спонтанное» употребляют в этом случае в связи с тем, что система сама, без нашего участия, выбирает несимметричное состояние, поскольку именно оно является энергетически наиболее выгодным. Из приведённого примера ясно, что если симметрия спонтанно нарушена, то вытекающие из неё законы сохранения и запреты не работают; в нашем примере это относится к сохранению углового момента. Подчеркнём, что полная симметрия теории может быть нарушена лишь частично: в нашем примере из полной симметрии относительно всех вращений в пространстве остаётся явной, ненарушенной симметрия относительно вращений вокруг направления магнитного поля.
 |
|
|
Рис. 6. Ненамагниченное (а) и намагниченное (б) состояния атомов железа. Стрелками показаны направления магнитных моментов атомов. Ненамагниченного начального состояния можно добиться, разогрев образец до высокой температуры, и быстро остудив. Из такого состояния образец всё равно перейдёт – в намагниченное: магнитным моментам атомов энергетически выгодно выстроиться. Выстроенные магнитные моменты создадут в образце магнитное поле, направленное так же, как магнитные моменты. |
Микроскопические существа, живущие внутри магнита, могли бы задать себе вопрос: «В нашем мире не все направления равноправны, угловой момент не сохраняется, но является ли пространство фундаментально несимметричным относительно вращений?» Изучив движение электронов и построив соответствующую теорию (в данном случае электродинамику), они бы поняли, что ответ на этот вопрос отрицателен: уравнения этой теории симметричны, но эта симметрия спонтанно нарушена за счёт «разлитого» вокруг них магнитного поля. Развивая эту теорию дальше, они бы предсказали, что поле, отвечающее за спонтанное нарушение симметрии, должно иметь свои кванты, фотоны. И построив внутри магнита маленький ускоритель, с радостью убедились бы, что эти кванты действительно существуют – они рождаются в столкновениях электронов!
В общих чертах ситуация в физике элементарных частиц похожа на ту, что мы только что описали. Но есть и важные отличия.
Механизм генерации масс частиц со спином 1 – в природе это W ±- и
Довольно прямолинейное обобщение механизма Энглера-Браута-Хиггса, связанное с включением в теорию фермионов и их взаимодействия с нарушающим симметрию скалярным полем, приводит к тому, что массы появляются и у фермионов. Всё начинает становиться на свои места! Стандартная модель теперь получается в результате дальнейшего обобщения путём включения не одного, а нескольких векторных полей – фотона, W ±- и
Вернемся в 1964 год. Для исследования свойств своей теории Энглер и Браут использовали довольно вычурный по сегодняшним меркам подход. Наверное поэтому они не заметили, что наряду с массивной частицей спина 1 эта теория предсказывает существование ещё одной частицы – бозона со спином 0. А вот Хиггс заметил, и сейчас эту новую бесспиновую частицу часто называют бозоном Хиггса. Как уже отмечалось, такая терминология не вполне корректна: ключевое предложение использовать скалярное поле для спонтанного нарушения симметрии и генерации масс частиц спина 1 впервые сделали всё же Энглер и Браут. Не вдаваясь больше в терминологию, подчеркнём, что новый бозон с нулевым спином является квантом того самого скалярного поля, которое нарушает симметрию. И в этом его уникальность.
Здесь нужно сделать уточнение. Повторим, что если бы спонтанного нарушения симметрии не было, то W ±- и
Эта арифметика, кстати, согласуется с тем, что все четыре поля Энглера-Браута-Хиггса – скалярные, их кванты имеют нулевой спин. Безмассовые W ±- и
Итак, бозон Хиггса – это квант одного из четырёх скалярных полей Энглера-Браута-Хиггса, существующих в Стандартной модели. Три других поедаются (научный термин!) W ±- и
4. А действительно ли нужен новый бозон?
Самое удивительное в этой истории заключается в том, что сегодня мы понимаем: механизм Энглера-Браута-Хиггса – отнюдь не единственный возможный механизм нарушения симметрий в физике микромира и генерации масс элементарных частиц, а бозон Хиггса мог бы и не существовать. Этому нас учит, в частности, физика конденсированных сред (жидкостей, твёрдых тел). В ней имеется множество примеров спонтанного нарушения симметрии и разнообразие механизмов этого нарушения. И в большинстве случаев ничего похожего на бозон Хиггса в этих примерах нет.
Ближайшим твердотельным аналогом спонтанного нарушения симметрий Стандартной модели в вакууме является спонтанное нарушение внутренней симметрии электродинамики в толще сверхпроводника. Оно приводит к тому, что в сверхпроводнике фотон в определённом смысле обладает массой (как W ±- и
Эффективная теория сверхпроводимости – теория Гинзбурга-Ландау – чрезвычайно похожа на теорию Энглера-Браута-Хиггса (точнее наоборот: теория Гинзбурга-Ландау на 14 лет старше). В теории Гинзбурга-Ландау тоже есть скалярное поле, которое однородно «разлито» по сверхпроводнику и приводит к спонтанному нарушению симметрии. Однако теорию Гинзбурга-Ландау недаром называют эффективной: она ухватывает, образно говоря, внешнюю сторону явления, но совершенно неадекватна для понимания фундаментальных, микроскопических причин возникновения сверхпроводимости. Никакого скалярного поля в сверхпроводнике на самом деле нет, в нём есть электроны и кристаллическая решетка, а сверхпроводимость обусловлена особыми свойствами основного состояния системы электронов, возникающими благодаря взаимодействию между ними 7.
Не может ли подобная картина иметь место и в микромире? Не может ли быть так, что никакого фундаментального скалярного поля, «разлитого» в вакууме, нет, а спонтанное нарушение симметрий вызвано совершенно иными причинами? Если рассуждать чисто теоретически и не обращать внимания на экспериментальные факты, то ответ на этот вопрос – утвердительный. Примером может служить так называемая «модель техницвета», предложенная в 1979 году уже упоминавшимся Стивеном Вайнбергом и независимо Леонардом Сасскиндом. В ней нет никаких фундаментальных скалярных полей, нет и бозона Хиггса. Вместо этого есть много новых элементарных частиц, по своим свойствам напоминающих известные кварки. Взаимодействие между этими новыми частицами и приводит к спонтанному нарушению симметрий и генерации масс W ±- и
Внимательный читатель может задать вопрос: «А как же с аргументами раздела 3.3, говорящими, что нарушать симметрию должно именно скалярное поле?» Лазейка здесь в том, что это скалярное поле может быть составным, в том смысле, что соответствующие ему частицы-кванты не элементарны, но состоят из других, элементарных частиц.
Вспомним в связи с этим квантовомеханическое соотношение неопределённостей Гейзенберга
Итак, при низких энергиях составная частица выглядит как элементарная. Для эффективного описания таких частиц при низких энергиях вполне можно считать, что они являются квантами некоторого поля. Если спин составной частицы равен нулю, то это поле будет скалярным.
 |
|
|
Рис. 7. Фотон большой длины волны и, значит, низкой энергии не способен разрешить структуру |
Подобная ситуация реализуется, например, в физике
Итак, скалярные поля, ответственные за спонтанное нарушение симметрий, могут в принципе быть составными. Именно такая ситуация предполагается в модели техницвета. При этом три бесспиновых кванта, которые поедаются W ±- и
Именно последнее обстоятельство привело к тому, что модель техницвета (по крайней мере в её изначальной формулировке) была отвергнута задолго до недавнего экспериментального обнаружения нового бозона: точные измерения свойств W ±- и
5. Открытие сделано. Что дальше?
 |
|
|
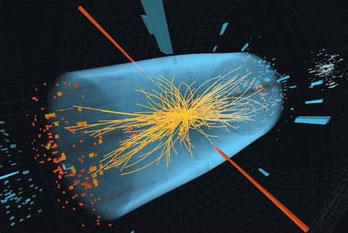
Рис. 8. Частицы, ускоренные в Большом адронном коллайдере до огромных энергий, сталкиваются, порождая множество вторичных частиц – продуктов реакции. Среди них был обнаружен и бозон Хиггса, который физики надеялись отыскать без малого полвека. |
Вернёмся, в качестве рабочей гипотезы, к минимальной версии теории – Стандартной модели с одним элементарным бозоном Хиггса. Поскольку в этой теории именно поле (точнее, поля) Энглера-Браута-Хиггса даёт массы всем элементарным частицам, взаимодействие каждой из этих частиц с бозоном Хиггса жёстко фиксировано. Чем больше масса частицы, тем сильнее взаимодействие; чем сильнее взаимодействие, тем более вероятен распад бозона Хиггса на пару частиц данного сорта. Распады бозона Хиггса на пары реальных частиц tt̃, ZZ и
То же можно сказать и о рождении бозона Хиггса в столкновениях протонов на Большом адронном коллайдере. Бозон Хиггса может рождаться в одиночку, или вместе с парой легких кварков высоких энергий, или вместе с одним W- или
Наконец, важным свойством бозона Хиггса является его взаимодействие с самим собой. Оно должно проявляться в процессе Н* → НН, где Н* – виртуальная частица. В Стандартной модели свойства этого взаимодействия тоже однозначно предсказываются. Впрочем, его изучение – дело отдалённого будущего.
Итак, на LHC имеется обширная программа исследования взаимодействий нового бозона. В результате её выполнения станет более или менее ясно, описывается ли природа Стандартной моделью или мы имеем дело с
6. Вместо заключения: в поисках «новой физики»
С «технической» точки зрения Стандартная модель внутренне непротиворечива. Это означает, что в её рамках можно – хотя бы в принципе, а как правило и на практике – вычислить любую физическую величину (разумеется, относящуюся к тем явлениям, которые призвана описывать Стандартная модель), и результат не будет содержать неопределённостей. Тем не менее, многие, хотя и не все, теоретики считают положение дел в Стандартной модели, мягко говоря, не вполне удовлетворительным. И связано это в первую очередь с её энергетическим масштабом.
Как ясно из предыдущего, энергетический масштаб Стандартной модели имеет порядок
В физике имеется ещё один масштаб энергий. Он связан с гравитацией и равен массе Планка
У обозначенной проблемы есть ещё один, более тонкий аспект. Он связан со свойствами физического вакуума. В квантовой теории вакуум – основное состояние природы – устроен совсем нетривиально. В нём всё время рождаются и уничтожаются виртуальные частицы, иными словами, образуются и исчезают флуктуации полей. Непосредственно наблюдать эти процессы мы не можем, но они оказывают влияние на наблюдаемые свойства элементарных частиц, атомов и т. д. Например, взаимодействие электрона в атоме с виртуальными электронами и фотонами приводит к наблюдаемому в атомных спектрах явлению – лэмбовскому сдвигу. Другой пример – поправка к магнитному моменту электрона или мюона (аномальный магнитный момент), тоже обусловленная взаимодействием с виртуальными частицами. Эти и подобные эффекты вычислены и измерены (в указанных случаях с фантастической точностью!), так что мы можем быть уверены, что имеем правильную картину физического вакуума.
В этой картине все параметры, изначально закладываемые в теорию, получают поправки, связанные с взаимодействием с виртуальными частицами. Их называют радиационными поправками. В квантовой электродинамике эти поправки малы, а вот в секторе Энглера-Браута-Хиггса они огромны. Такова особенность элементарных скалярных полей, составляющих этот сектор; у других полей этого свойства нет. Главный эффект здесь состоит в том, что радиационные поправки стремятся «подтянуть» энергетический масштаб Стандартной модели MSM к гравитационному масштабу MPl . Если оставаться в рамках Стандартной модели, то единственный выход – подобрать изначальные параметры теории так, чтобы вместе с радиационными поправками они приводили к правильному значению MSM . При этом выясняется, что точность подгонки должна составлять величину, близкую к
Многие (хотя, повторим, не все) теоретики считают, что эта проблема однозначно свидетельствует о необходимости выхода за рамки Стандартной модели. Действительно, если Стандартная модель перестаёт работать или существенно расширяется на энергетическом масштабе MNP (NP – «new physics»), то аргумент о радиационных поправках модифицируется. Требуемая точность подгонки параметров в этом случае составляет, грубо говоря, M 2SM / M 2NP , а на самом деле на пару порядков слабее. Если считать, что тонкой подстройки параметров в природе нет, то отсюда следует, что масштаб «новой физики» должен лежать в области
Какой могла бы быть «новая физика»? Единства у теоретиков по этому поводу нет. Один вариант – составная природа скалярных полей, обеспечивающих спонтанное нарушение симметрии. О нём мы говорили в разделе 4. Другая, тоже популярная (пока?) возможность – суперсимметрия. На ней мы останавливаться не будем; скажем только, что суперсимметрия предсказывает целый зоопарк новых частиц с массами в области сотен ГэВ – нескольких ТэВ. Обсуждаются и весьма экзотические варианты вроде дополнительных измерений пространства (скажем, так называемая
Несмотря на все усилия, до сих пор никаких экспериментальных указаний на «новую физику» получено не было. Это,
7. Приложение. Коллайдеры высоких энергий
Физика элементарных частиц, которая изучает самые крошечные объекты в природе, нуждается в гигантских исследовательских установках, где эти частицы ускоряются, сталкиваются, распадаются. Самые мощные из них – коллайдеры.
Коллайдер – ускоритель со встречными пучками частиц, в котором частицы сталкиваются «лоб в лоб». В электрон-позитронных коллайдерах (другое название –
Большой адронный коллайдер (LHC) – протон-протонный, он ускоряет два пучка протонов один навстречу другому (может также работать и как тяжелоионный коллайдер). Проектная энергия протонов в каждом из пучков составляет 7 ТэВ, так что полная проектная энергия столкновения – 14 ТэВ. В 2011 году LHC работал на половине этой энергии, т. е. полная энергия столкновения составляла 7 ТэВ, а в 2012 году – на полной энергии 8 ТэВ. LHC представляет собой кольцо длиной 27 км, в котором протоны ускоряются электрическим полем, а удерживаются магнитным полем, создаваемым сверхпроводящими магнитами. Столкновения протонов происходят в четырёх местах, где расположены детекторы, регистрирующие частицы, рождающиеся в этих столкновениях. Два из этих детекторов – ATLAS и CMS – предназначены для исследований в области физики элементарных частиц при высоких энергиях, а два других –
Spp̃S – протон-антипротонный коллайдер в ЦЕРНе. Длина кольца – 6,9 км, максимальная энергия столкновения – 630 ГэВ. Работал с 1981 по 1990 год.
LEP – кольцевой электрон-позитронный коллайдер с максимальной энергией столкновения 209 ГэВ, расположенный в том же туннеле, что и Большой адронный коллайдер. Работал с 1989 по 2000 год.
SLC – линейный электрон-позитронный коллайдер в SLAC, США. Энергия столкновения – 91 ГэВ (масса
Tevatron – кольцевой протон-антипротонный коллайдер в Fermilab, США. Длина кольца 6 км, максимальная энергия столкновения – 2 ТэВ. Работал с 1987 по 2011 год.
Сравнивая протон-протонные и протон-антипротонные коллайдеры с электрон-позитронными, нужно иметь в виду, что протон – составная частица, он содержит в себе кварки и глюоны. Каждый из этих кварков и глюонов несёт лишь часть энергии протона. Поэтому в случае Большого адронного коллайдера, например, энергия элементарного столкновения (между двумя кварками, между двумя глюонами или кварка с глюоном) заметно ниже суммарной энергии сталкивающихся протонов (14 ТэВ при проектных параметрах).
Плюс протон-протонных (и протон-антипротонных) коллайдеров в том, что даже с учётом этой особенности достичь высоких энергий столкновений на них технически проще, чем на электрон-позитронных. Есть и минус.
1 См. «Наука и жизнь» № 1, 1996 г., «Бозон Хиггса необходим!» (Примеч. ред. «НиЖ»)
2 Стандартная модель на самом деле заведомо неполна, но это предмет отдельного разговора. Отметим только, что о её неполноте свидетельствуют данные космологии – науки о Вселенной. Проявится ли неполнота Стандартной модели при энергиях LHC – вопрос пока открытый и интригующий.
3 Применение тильды для обозначения античастиц – правило не строгое. Электрон и его античастицу позитрон принято обозначать символами e– и e+ соответственно. То же относится к мезонам и
4 В реальном мире для ограниченного (но только ограниченного!) круга процессов так оно и есть. Например, взаимодействие быстрого массивного электрона, спин которого направлен против направления движения, с покоящейся или медленно движущейся мишенью (скажем, атомным ядром), практически не отличается от взаимодействия левого безмассового электрона.
5 Противоречия с утверждением, сделанным в предыдущей сноске, здесь нет: мишень, покоящаяся в старой системе отсчёта, теперь движется быстрее электрона, и в реальном мире взаимодействие электрона с подобной мишенью существенно отличается от взаимодействия с покоящейся мишенью.
6 Похожие механизмы стали известны раньше в физике конденсированных сред благодаря работам Г. и Ф. Лондонов, В. Л. Гинзбурга и Л. Д. Ландау, Н. Н. Боголюбова, П. У. Андерсона, теории Бардина-Купера-Шриффера и других.
7 См. «Наука и жизнь» № 2, 2004 г., «Сверхпроводимость и сверхтекучесть», http://www.nkj.ru/archive/articles/4751/ (Примеч. ред. «НиЖ»)
8 См. «Наука и жизнь» №№ 2, 3 1997 г., «Суперструны: на пути к теории всего» (Примеч. ред. «НиЖ»)
(См. так же на сайте «Разум или вера?»:
Некоторые пояснения к терминам
Стандартное отклонение (среднеквадратичное отклонение) σx – характеристика случайных отклонений измеренной величины от среднего значения. Вероятность того, что измеренное значение величины X случайным образом окажется отличающимся на 5σx от истинного, составляет всего 0,00006%. Именно поэтому в физике элементарных частиц отклонение сигнала от фона на σx считают достаточным для признания сигнала истинным.
Частицы, перечисленные в Стандартной модели, кроме протона, электрона, нейтрино и их античастиц, нестабильны: они распадаются на другие частицы. Впрочем, два типа нейтрино из трёх тоже должны быть нестабильными, но их время жизни чрезвычайно велико. В физике микромира действует принцип: всё, что может происходить, действительно происходит. Поэтому стабильность частицы связана с
С барионным числом связана ещё одна внутренняя симметрия. Точная она или приближённая, стабилен ли протон или имеет конечное, хотя и очень большое время жизни – предмет отдельного разговора.
Кварки – один из типов элементарных частиц. В свободном состоянии они не наблюдаются, а всегда связаны друг с другом и образуют составные частицы – адроны. Единственное исключение –
b-кварк – один из шести типов кварков, второй по массе после
Мюон – тяжёлый нестабильный аналог электрона с массой
Виртуальная частица отличается от реальной тем, что для реальной частицы выполняется обычное релятивистское соотношение между энергией и импульсом E2 =
Лэмбовский сдвиг уровней – небольшое отклонение тонкой структуры уровней атома водорода и водородоподобных атомов под действием испускания и поглощения ими виртуальных фотонов или виртуального рождения и аннигиляции электрон-позитронных пар. Эффект обнаружили в 1947 году американские физики У. Лэмб и Р. Резерфорд.
|
|
|
|